平面几何数学基础
0. 概要
这篇文章讲解了在对机械臂进行运动学求解时所需的数学知识,大多都是高中数学基础,向量相关的属于大学线性代数的内容。希望你可以耐心看下去,这对你理解后面的算法有帮助。
如果对公式推导的详细过程有困难,可以暂时跳过,记住结论即可。
1. 三角函数
1.1 三角函数基础
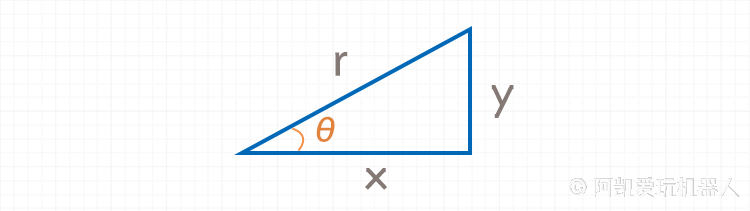
1.2 正切与反正切

1.3 arctan2
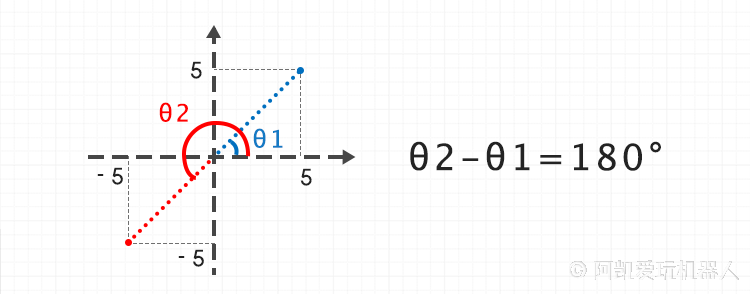
上面的公式没有考虑
为了解决这个问题,我们需要引入另外一个函数
这个函数分别传入
所以
1.4 已知AB求夹角
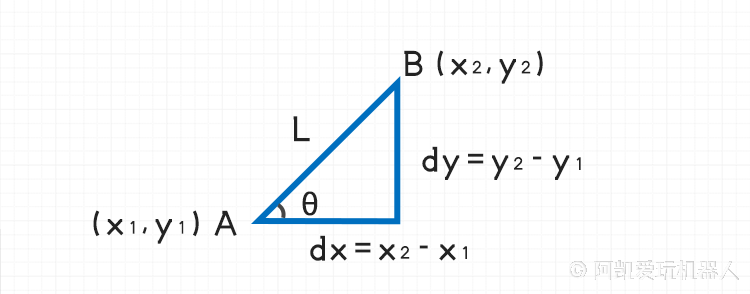
如果已知
求
1.5 已知一点、直线和夹角,求另一点
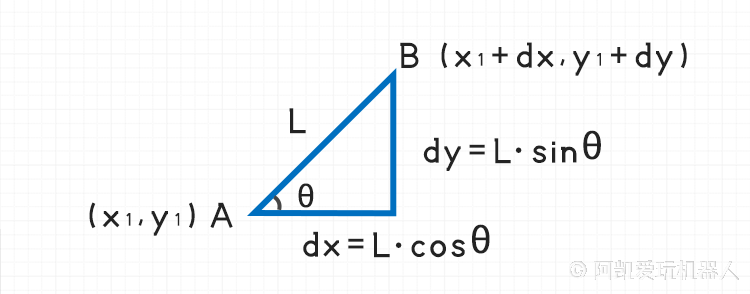
如果
1.6 余弦公式 - 已知三边求夹角
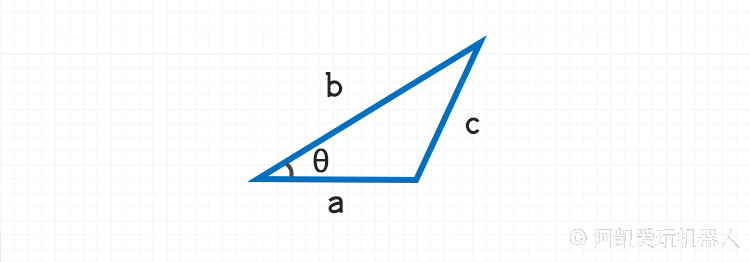
三边求夹角的Python实现代码
import math
def cal_tri_angle(a, b, c):
'''返回边a与边b之间的夹角,弧度制'''
try:
theta = math.acos((a**2 + b**2 - c**2) / (2 * a * b))
except ValueError as e:
print(e)
print('a={}, b={}, c={}'.format(a, b, c))
exit(-1)
return theta
2. 向量
向量叉乘主要用于辅助筛选候选的关节坐标,判断关节是朝外,还是朝里。
2.1 向量叉乘 (叉积)
我们不光要知道向量与向量之间的夹角是多少,而且想知道,从向量
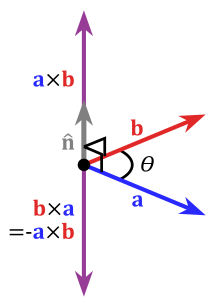
向量
向量
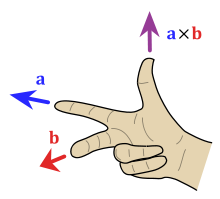
如果向量
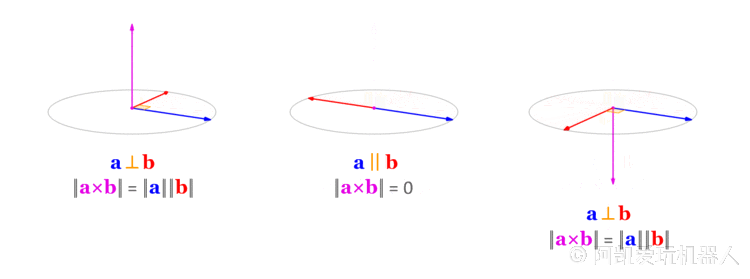
另外向量叉乘满足反交换率,叉乘的顺序先后不一样,得到的向量方向相反。
二维坐标系下叉乘的计算与几何含义
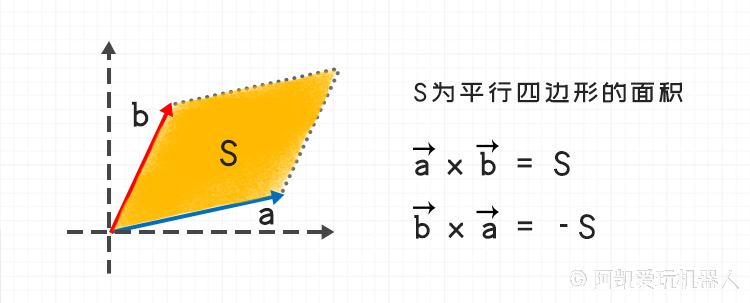
叉乘的几何意义是以两向量为邻边的 平行四边形的有向面积 。
如果
则说明,从向量
说明从向量
Python代码片段如下:
def vector_cross_product(x1, y1, x2, y2):
'''向量叉乘'''
return x1 * y2 - x2 * y1
def is_vector_ccw(x1, y1, x2, y2):
'''向量a是否是逆时针旋转到向量b'''
return vector_cross_product(x1, y1, x2, y2) > 0
2.2 叉乘矩阵
将两个向量之间的叉乘运算改写为 叉乘矩阵 与向量的乘积。
定义运算符
向量叉乘可以改写为矩阵与向量乘积的形式
所以叉乘又可以写为
3. 圆
通过计算得到圆与圆之间的交点,作为关节坐标, 然后辅助上面介绍的叉乘, 对关节坐标进行筛选。
3.1 圆的表达式
圆有两种表示:
圆的标准方程
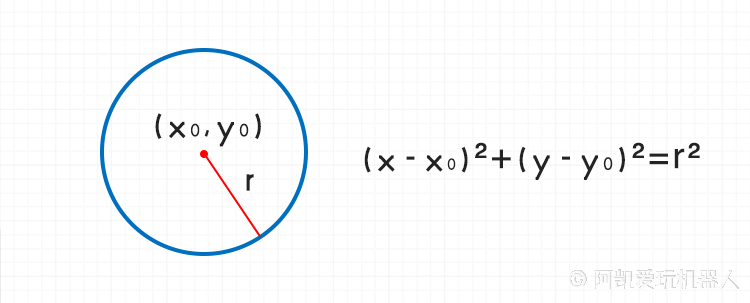
其中
圆的参数方程
3.2 两个圆求交点
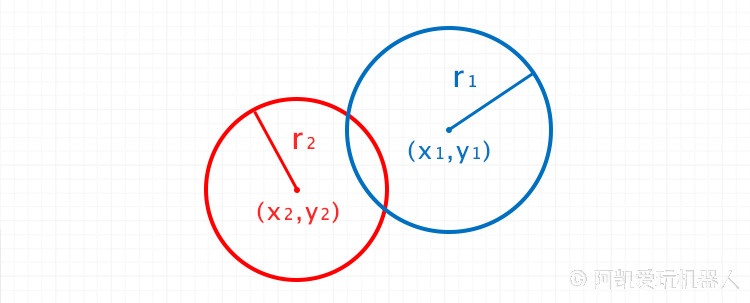
圆1用参数方程表示,圆2用标准方程表示。
为什么要这样做? 这样减少展开项的复杂度
圆1
圆2
把圆1的方程带入圆2的方程
展开之后整理得到
令
公式
且三角函数有如下属性
展开得到
令
公式
这是关于
首先判断是否
如果大于0则说明两个圆之间有交点,此方程组可解,根据二元一次方程组的公式可得
其中
接下来如果想继续求交点,就必须把
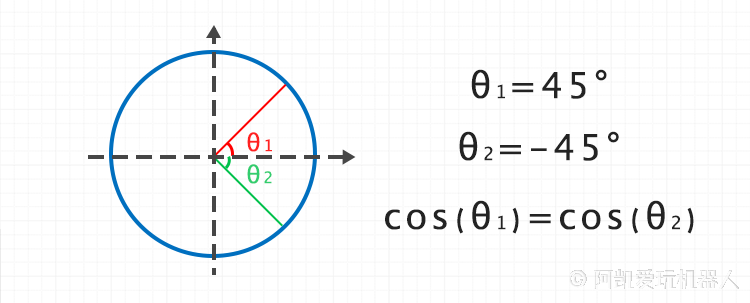
把
得到交点
然后再判断
判断
求解两个圆之间交点的代码
src/geometry_utils.py
import math
def circle_inter_posi(x1, y1, r1, x2, y2, r2):
'''
圆之间的交叉点
'''
distance = math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
if distance > (r1 + r2) or (x1 == x2 and y1 == y2):
print('Error: circle has not intersect points')
return False, None
else:
pass
# print('distance: {}'.format(distance))
a = 2 * r1 * (x1 - x2)
b = 2 * r1 * (y1 - y2)
c = (r2**2 - r1**2) - (x1 - x2)**2 - (y1 - y2)**2
p = a**2 + b**2
q = -2 * a * c
r = c**2 - b**2
cos_theta_1 = (-q + math.sqrt(q**2 - 4*p*r))/ (2 * p)
cos_theta_2 = (-q - math.sqrt(q**2 - 4*p*r))/ (2 * p)
# 存放所有可能的角度
angle_list = []
if abs(cos_theta_1) < 1:
angle_list.append(math.acos(cos_theta_1))
if abs(cos_theta_2) < 1:
angle_list.append(math.acos(cos_theta_2))
# 把角度负值也添加到angle_list中
for i in range(len(angle_list)):
theta = angle_list[i]
if theta == 0.0:
# 如果角度为0则不需要反转,因为-0跟0是同一个角度
continue
angle_list.append(-1*theta)
angle_list = list(set(angle_list))
# 存放交点
result = []
# 遍历验证角度是否正确
for angle in angle_list:
ix = x1 + r1 * math.cos(angle)
iy = y1 + r1 * math.sin(angle)
if abs(math.sqrt((ix-x2)**2 + (iy-y2)**2)-r2) <= 1e-3:
result.append((ix, iy))
return True, result